1. Definice šumového čísla - obr. 1:

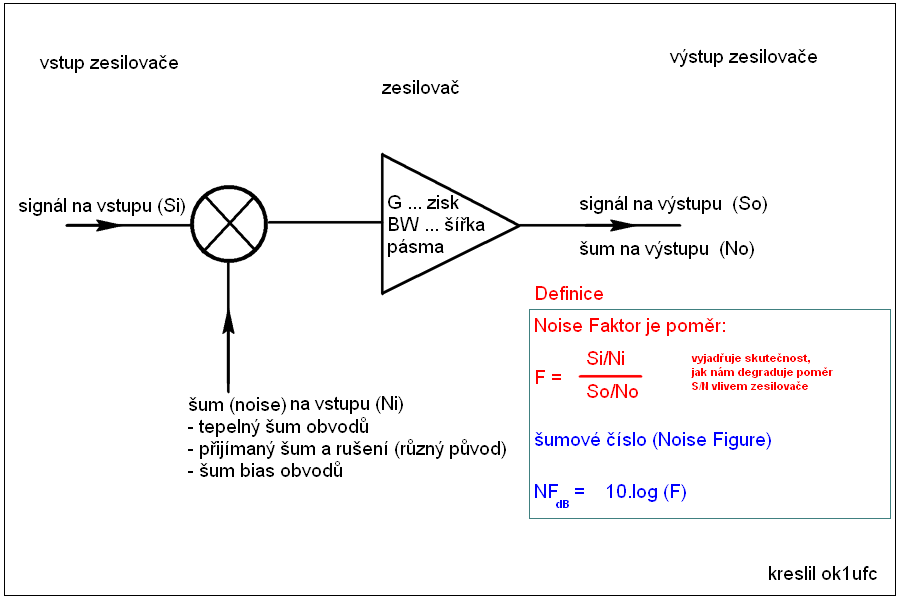
Začneme s výstupem zesilovače, který na výstupu produkuje užitečný signál So a také šum No. Na vstupu uvažujme, že do zesilovače je přiveden užitečný signál Si a současně také různé druhy šumů Ni. Šum má různý původ, přijímáme ho, dodáváme si ho z bias obvodů a také nám na každém rezistoru vzniká tzv. tepelný šum.

Nicméně, jsme nyní schopni vydefinovat dva důležité parametry, tzv. Noise Faktor (nevím, jak se to správně jmenuje česky, už jsem dlouho nechodil do školy) F = (Si/Ni) / (So/No). Noise Faktor je číslo větší než 1 a říká nám, jak nám v každém použitém zesilovači degraduje odstup signál/šum (S/N). Ten je vlivem degradace v zesilovači vždy na výstupu horší, jmenovatel zlomku je tedy vždycky menší než čitatel a šumový faktor musí být tedy vždycky větší, než 1.

Šumové číslo (Noise Figure - NF dB = 10 x log (F). Protože log (1) = 0, je číselně šumové číslo v dB vždy větší než 0. Za Ultra LNA budu považovat LNA s NF menším než 0.5 dB a skutečnost, že za určitých konstrukčních podmínek lze naměřit NF = 0.15 dB. Tuto definici šumového čísla jsem si nevymyslel, byla používána v amerických pramenech, podle autora FRIISE. V německých pramenech byl používán způsob navržený FRANZEM. Pro účel následně popsané metody měření zůstanu u Friisovo definice, protože s ní vystačím. Vše je stručně a názorně shrnuto na obrázku nahoře.

2. Úvaha o úpravě definičního vzorce pro srovnávací metodu měření

Uvažujme příklad, ve kterém máme dva nízkošumové předzesilovače LNA1 a LNA2.

a) označme si šumový faktor každého z nich jako F1 = ((S/N)/(S1/N1)) a obdobně
b) šumový faktor F2 = ((S/N)/(S2/N2)),

kde v obou vztazích bude hrát roli stejný generátor připojený na vstup. Se stejným odstupem signál/šum S/N. Výstupy z každého předzesilovače však budeme přepínat a do TCVRu pustíme vždy jen jeden. Na výstupu TCVRu (vypnuté AGC, atd. popíšu v části měření) připojíme spektrální analyzátor nízkofrekvenčního spektra (program pro zvukovku na PC), na kterém se budeme snažit odečíst postupně poměry signál/šum pro každý předzesilovač, tj. S1/N1 a S2/N2.

Aby bylo zjevné, proč to dělám, provedeme jednoduchou školní početní operaci s oběma vzorci. A sice roznásobíme každý z nich jmenovatelem svého zlomku. A dostaneme toto:

S/N = F1 x (S1/N1) a také S/N = F2 x (S2/N2), kde v obou vzorcích je S/N stejné (stejný generátor, stejné nastavení, stejné kabely, stejný výstup, prostě všechno je pro oba LNA na vstupu naprosto stejné. Potom si můžeme dovolit vyzkoušet algebraické porovnání:

F1 x (S1/N1) = F2 x (S2/N2) a s rovnicí vyvedeme podělením (S1/N1) tento zápis: F1 = F2 x (S2/N2)/(S1/N1)

Z rovnice je zřejmé, že když známe (např. máme přesně změřené) šumové číslo předzesilovač LNA2, tedy NF2, resp. noise faktor F2, měli bychom být schopni srovnávací metodou na spektrálním analyzátoru zjistit šumové číslo NF1, resp. noise faktor F1 předzesilovače LNA1. Teď už bychom si asi poradili, ale jednodušší práci budeme mít, když si předchozí rovnici (tuto: F1 = F2 x (S2/N2)/(S1/N1) ) upravíme dekadickým logaritmováním a násobením 10. Tak, jako bylo definováno šumové číslo NF (v dB) v prvním odstavci.
Matematikou nepolíbení si připomenou, že součiny logaritmů se mění na součty. Vyjde nám vzorec uvedený dále a s tím budeme dělat.

3. Definiční vzorec šumového čísla platný pro srovnávací metodu

10 x log (F1) = 10 x log (F2) + 10 x log ((S2/N2)/(S1/N1)) nebo také 10 x log (F2) = 10 x log (F1) - 10 x log ((S2/N2)/(S1/N1))
ve vzorcích nahradíme 10 x log (F1) hodnotou šumového čísla NF1 (dB), hodnotu 10 x log (F2) hodnotou šumového čísla NF2 (dB) a podíly signál/šum rozdílem jejich hodnot v dB.

Dostaneme hezký vzorec, se kterým se dá dělat prostým odečítáním z grafů, ve kterých budeme muset maximálně odečíst úrovně v dB:

NF1 (dB) = NF2 (dB) +  S2/N2 (dB) - S1/N1 (dB)

Co na první pohled ze vzorce vidíme?

a) Pokud máme poměry S2/N2 a S1/N1 stejné, musí být stejná šumová čísla NF1 a NF2 (no, to je teda objev, hi).
b) Pokud máme poměr S2/N2 (dB) vyšší než S1/N1 (dB), je šumové číslo NF1 (dB) předzesilovače LNA1 horší. A to o rozdíl v poměrech Sout/Nout vyjádřený v dB.

Polopaticky můžeme tvrdit. že když známe rozdíl v odstupu signál/šum (S/N) v decibelech u dvou LNA a alespoň hodnotu šumového čísla (NF v dB) jednoho z předzesilovačů, pak pouhým přičtením (nebo odečtením) rozdílu v odstupu S/N můžeme stanovit hodnotu šumového čísla druhého předzesilovače. Vyšší šumové číslo má předzesilovač s horším odstupem S/N.

No, mohli bychom toho předpokládat víc, když se zamyslíme, jak vypadají slaboučké signály a šumy na spektrálním analyzátoru. Ale to až v praktické části.

Poznámka: Tento článek byl upraven z původního, který jsem publikoval v roce 2017 v jiné publikaci zde.

TU 73, Mira, ok1ufc