|
Aktualizováno v dubnu 2020 |
||
| |
||
| |
||
| Definice šumového čísla přijímače podle pana Franze | ||
Druhá definice šumového čísla přijímače byla definována Franzem. Autor předpokládal, že zdrojem šumu v přijímači jsou reálné složky impedancí v zesilovacím retězci a aktivní prvky (tehdy elektronky, dnes polovodičové materiály). Pan Franz rovněž předpokládal, že největší podíl mají šumy vzniklé ve vstupních obvodech. Dále předpokládal, že šum v rezistorech je termického původu, že v každé látce jsou molekuly, které jsou v neustálém a nepravidelném pohybu. Stanovil, že mírou pohybu je teplota, že při absolutní nule (-273.15 °C = 0 K) veškerý pohyb ustane. Pohybem molekul se však přemisťují elektrické náboje (např. v kusu drátu) a mezi dvěma různými body se na takovém vodiči dá naměřit napětí. Napětí je střídavé, neustále mění velikost i směr. Proto na takovém vodiči, chcete-li, rezistoru vzniká směs střídavých napětí v celém kmitočtovém spektru. Většina takových napětí se však ve vodiči vyrovná uvnitř a navenek se projevuje velice malou hodnotou. Tak nás učili kdysi ve škole. Věřil jsem tomu a nikdy jsem nebyl fyzikem a ani jsem předchozí teorii neověřoval žádným experimentem.
Definice šumového čísla podle Franze
Nápodobně jsem věřil tomu, že výkon šumu, který vzniká na odporu má
velikost:
Pš = 4 * k * T * B, kde k je tzv. Bolzmanova konstanta k = 1.38*10-23 a rozměr je W/K (pokud hovoříme o výkonu, mezi SI jednotkami se udává v rozměru J/K, pokud se hovoří o energii a platí, že 1J = 1 Wattsekunda), T je absolutní teplota v Kelvinech a B je šířka pásma v Hz, na které zkoumáme výkon šumu.
Také nás učili, že výkon P = U*I a lze ho vyjádřit s použitím Ohmova zákona jako P = U2/R
Pokud vyjádříme šumové napětí Uš z výkonu, získáme tento
vzoreček:
Uš = Odmocnina (4*k*T*B*R)
Takové napětí bychom obdrželi na nezatíženém odporu, z kterého bychom
neodebírali žádný proud. Pokud uvažujeme s nejúčinnějším přenosem výkonu
při účinném přizpůsobení, kdy platí, že Zg = Zload (impedance zdroje Zg je
stejná jako impedance zátěže Zload), potom šumový výkon na vstupu ideálně
přizpůsobeného vstupního zesilovače bude:
Pi = Pš/4 = k*T*B a vstupní napětí musí být Ui =
Odmocnina (k*T*R*B)
To znamená, že připojíme-li na vstup ideálního přijímače bez šumu
přizpůsobenou anténu (nebo rezistor), předává nám taková anténa do
přijímače šumový výkon:
Pant = Pš/4 = 1*k*T (ve W/Hz) na každý Hz
šířky pásma.
Pokud je na vstupu přijímače také užitečný signál, který má stejnou
hodnotu, jako šum, považujeme tuto hodnotu za tzv. mezní hodnotu
citlivosti RX.
Polopaticky řečeno, šumové číslo vyjádřené v násobcích 1*kT
udává, kolikrát je vlastní šum přijímače RX větší, než 1*kT na 1Hz
šířky pásma.
Toto (předchozí odstavec) je definice šumového čísla podle Franze.
Co se děje s výkonem šumu na vstupu zesilovače?
Na vstupu RX uvažujme velikost šumového výkonu o velikosti
Pi = k*T*B
Dále uvažujme totéž, co jsme uvažovali u definice šumového faktoru v
úvaze odvozené na základě poznatků pana Friise.
Tedy, přijímačem (zesilovačem) dojde k zesílení signálu A krát (A
je zesílení vyjádřené jako poměr, tedy kolikrát, ne zisk v dB).
Zesílením v zesilovači (přijímači) také dojde k zesílení vstupního šumu
F krát. F je tzv. Noise Faktor, šumový faktor zesilovače, který
nám udává, kolikrát bude signál při zesílení znehodnocen šumem (tedy
kolikrát se zhorší odstup S/N). Potom můžeme napsat rovnici:
Pout = k*T*B*G*F a aby se s takovou rovnicí dalo
dělat prakticky, provedeme jednoduchou algebraickou úpravu. K pravé straně
odečteme a hned zas přičteme, aby se nezměnila platnost rovnice, stejné
číslo k*T*B*G a rovnice bude potom vypadat takto:
Pout = k*T*B*G*F - k*T*B*G + k*T*B*G,
no, s tím se toho ještě taky nedá moc dělat, ale vytkneme z prvních dvou
sčítanců k*T*B*G a přepíšeme rovnici do pohlednější podoby:
Pout = (F-1)*k*T*B*G + k*T*B*G; no to je teda objev!
Vyrobili jsme rovnici pro ideální bezšumový přijímač (zesilovač), ke
kterému na vstupu přičítáme šumový výkon.
Porovnejme si úvahu s článkem o definici
šumu podle Friise. Je tam jediný obrázek, ve kterém jsem si ideální
zesilovač (který nemá na vstupu šum) doplnil o zdroj šumu, který jsem
přičetl na vstupu k užitečnému signálu. Na uvedené stránce je tento
obrázek:
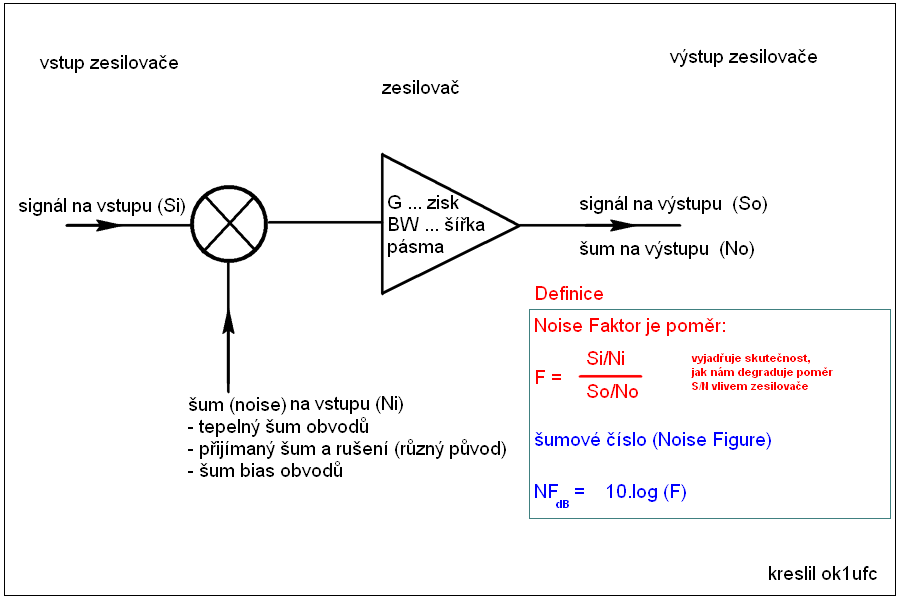
Jak vidíme, provedl jsem v předchozím vztahu pouze důkaz
použité úvahy.
