|
Poslední aktualizace 2021 |
||
|
|
|
|
| |
||
| Keplerian Elements - značení a význam kepleriánských dat | ||
Úvod
Radioamatérský provoz s využitím satelitů existuje několik desítek let. Za dobu jejich používání se rozšířil soubor pomůcek, pomocí kterých můžeme stanovit vůči našemu stanovišti (QTH, Observer, ...) polohu satelitu na oběžné dráze. Za velice užitečné však považuji porozumět těm nejnutnějším základům, které pojednávají o orbitální mechanice a o tzv. "keplerian elements".
Historie
V orbitální mechanice Keplerova rovnice
popisuje různé geometrické vlastnosti oběžné dráhy satelitu (obecně
nebeského tělesa) vystaveného centrální přitažlivosti, v případě satelitů
obíhajících kolem země přitažlivosti zemské.
Poprvé rovnici odvodil Johannes Kepler v roce 1609 v kapitole 60 své
Astronomia nova a v V. knize jeho Epitome of Copernican Astronomy (1621).
Kepler navrhl iterativní řešení rovnice. Rovnice hrála důležitou roli v
historii fyziky i matematiky, zejména klasické nebeské mechaniky a hraje
ji dodnes.
TLE v současnosti
Soudobé programy používají tzv. TLE (Two-line
element set - Wikipedia), které obsahují sedm nebo osm
Keplerovských prvků, jejichž význam popisuji dále.
Sedm nebo osm Keplerovských prvků
Učebnici základů jsem volně převzal od N6NKF (Franklin Antonio), který ji uvedl ve svém původním manuálu ke svému SW (Instant Tracks) pracujícího pod MS-DOS. Později ji nezisková organizace AMSAT použila na svých stránkách https://www.amsat.org/keplerian-elements-tutorial/ . Protože se jedná o vynikajícím způsobem stručně zpracované dílo, dovolil jsem si význam volně přeložit a doplnit několika ilustracemi.
Orientace na oběžné dráze a vůči zemi
Obrázek je určen k tomu, abychom se orientovali v základních věcech, to je v rovinách a úhlech. Pracujeme s rovinou zemského rovníku. Ta je označená červeně. Pracujeme s rovinou oběžné dráhy satelitu. Ta je označená modře. Obě roviny se protínají v průsečnici, což je úsečka vymezená průsečíky oběžné dráhy s rovinou rovníku. Průsečíky jsou dva, ale jeden z nich je označen jako vzestupný bod. Vzestupný bod se nazývá proto, že tímto bodem vstoupí satelit nad severní polokouli Země.
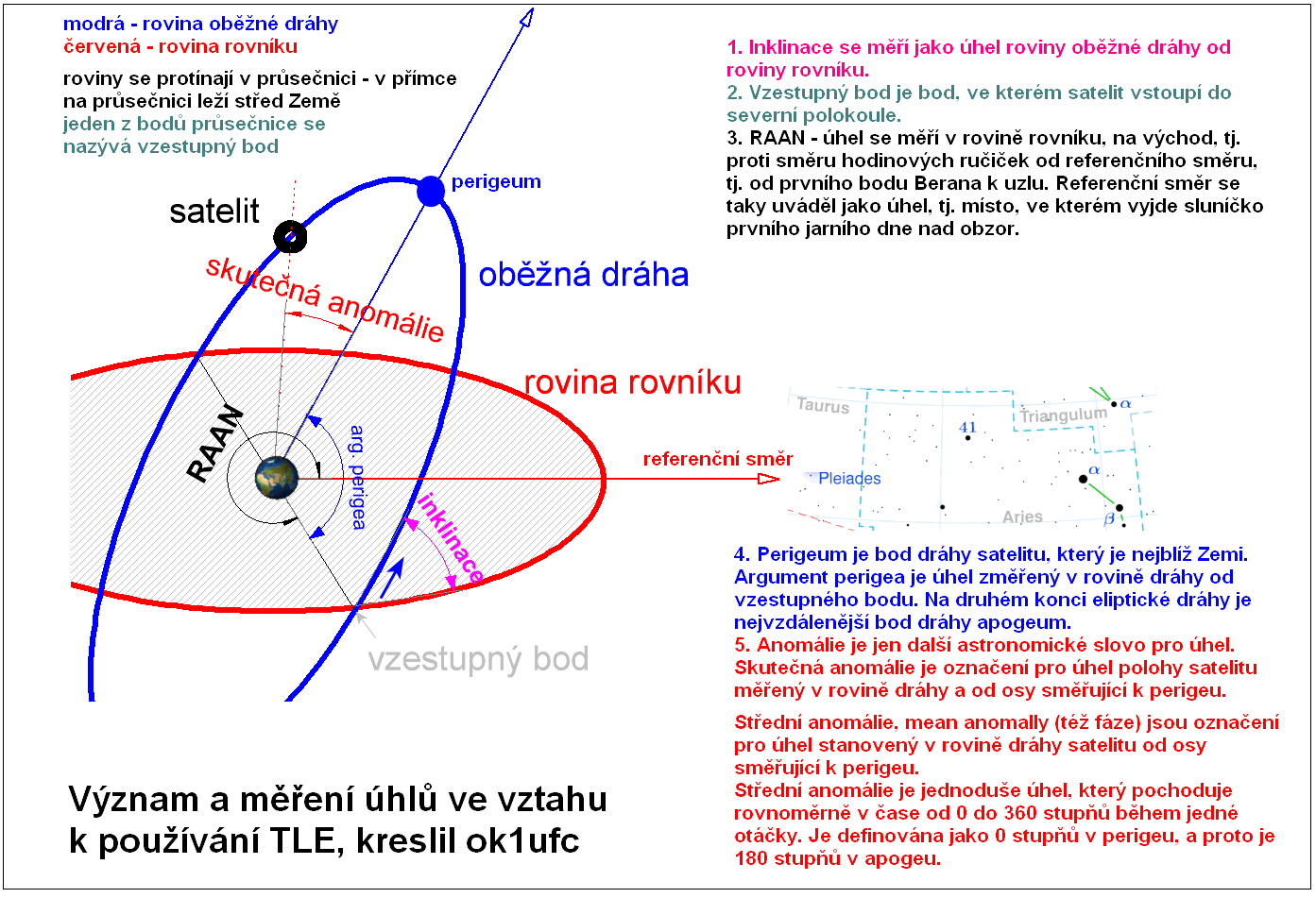
K určení oběžné dráhy satelitu je zapotřebí sedm čísel. Tato sada sedmi čísel se nazývá orbitální elementy satelitu, nebo taky "keplerovské" prvky, Keplerian Elements nebo prostě jen prvky. Ta čísla definují elipsu, orientují ji kolem Země a umístí satelit na elipsu v určitém čase. Sada orbitálních elementů je tedy snímek oběžné dráhy satelitu v určitém čase.
V Keplerově modelu obíhají satelity v elipse
konstantního tvaru a orientace. Země je v jednom ohnisku elipsy, ne ve
středu (pokud není elipsa oběžné dráhy ve skutečnosti dokonalým kruhem).
Skutečný svět je o něco složitější než Keplerův model a sledovací programy
to kompenzují zavedením drobných korekcí do Keplerova modelu. Tyto korekce
jsou známé jako poruchy, pertubace. Perturbace, o kterých satelitní
sledovací programy vědí, jsou způsobeny nekonzistencí gravitačního pole
Země (kterou naštěstí nemusíte specifikovat) a "bržděním" satelitu v
důsledku atmosféry. Brždění se tak stává volitelným osmým orbitálním
prvkem.
Dále autor píše, proč orbitální prvky zůstávají pro většinu lidí záhadou.
Domnívá se, že je to způsobeno jednak averzí mnoha lidí k myšlení ve třech
dimenzích a zadruhé hroznými jmény, která dali astronomové těmto sedmi
jednoduchým číslům a několika souvisejícím pojmům. Prý, aby toho nebylo
málo, tak se k určení stejného čísla používá několik různých jmen a
názvosloví se stalo nejtěžší částí nebeské mechaniky :-)
Osm čísel keplerovských dat
|
Původní název |
Můj překlad do češtiny |
|
Epoch |
Epocha, nezní mi to dobře, čas T0 je hezčí |
|
Orbital Inclination |
Inklinace - sklon oběžné dráhy |
|
Right Ascension of Ascending Node (R.A.A.N.) |
RAAN - úhel, viz obrázek a definice v textu níž |
|
Argument of Perigee |
Argument perigea - úhel měřený v rovině dráhy satelitu, viz obrázek, kde rovina není příliš vidět |
|
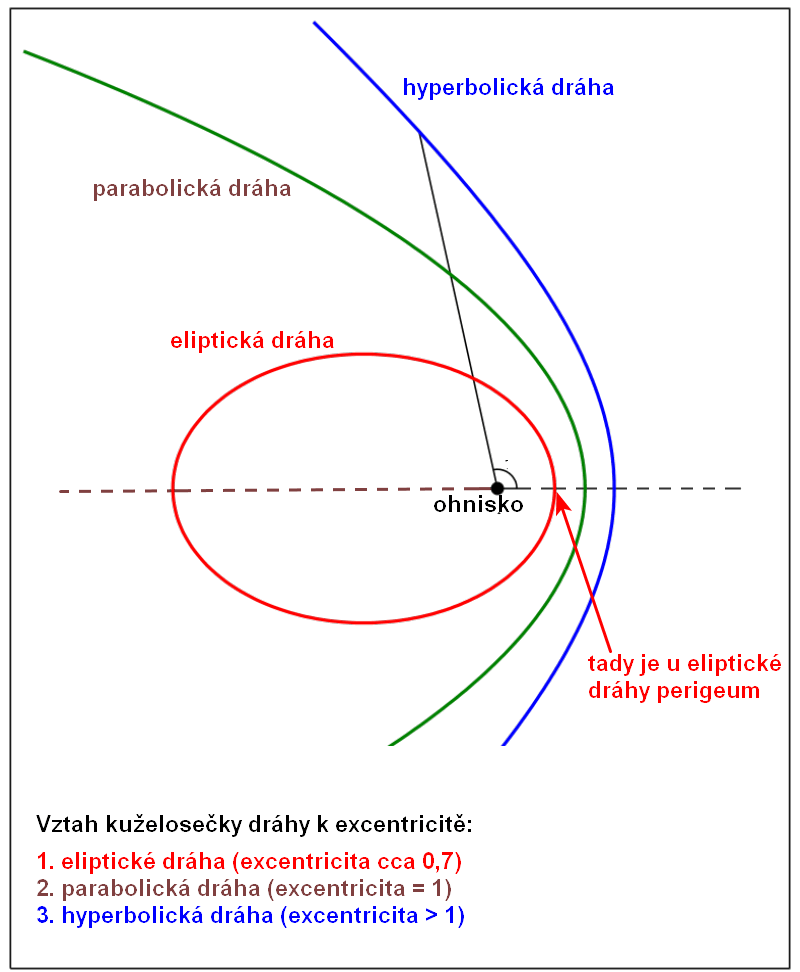
Eccentricity |
Excentricita - viz obrázek dole |
|
Mean Motion |
Střední pohyb |
|
Mean Anomaly |
Fáze, taky střední anomálie, anomálie mi nezní dobře |
|
Drag (optional) |
Drag - brždění (potažení, posun, brždění jsem si vymyslel, je však jednou z příčin) |
Pár slov k významu jednotlivých čísel
Epocha
(také známé jako "Epoch Time" nebo "T0")
Epocha je jednoduše číslo, které určuje čas, kdy byl snímek pořízen.
Inklinace - sklon oběžné dráhy
(také znám jen jako "Sklon" nebo "I0")
Elipsa oběžné dráhy leží v rovině nazývané jako orbitální rovina. Rovina
oběžné dráhy vždy prochází středem Země, ale může být nakloněna libovolným
úhlem vzhledem k rovníku. Sklon je úhel mezi rovinou oběžné dráhy a
rovinou rovníku. Podle konvence je sklon číslo mezi 0 a 180 stupni.
Podrobnosti o inklinaci jsou na
Orbital inclination - Wikipedia
. Dočteme se o dalších pojmech, o tom, co je myšleno dráhou
rovníkovou, polární, co se nazývá dráhou prográdní, retrográdní, čím se
vyznačuje dráha kritická (inklinace = 63,4°).
Základní pojmy: Dráhy se sklonem blízkým 0 stupňům se nazývají rovníkové
dráhy (protože satelit zůstává téměř nad rovníkem). Oběžné dráhy se
sklonem blízkým 90 stupňům se nazývají polární (protože satelit prochází
přes severní a jižní pól). Průsečík rovníkové roviny a orbitální roviny je
přímka, která se nazývá přímka uzlů.
Existuje mnoho účelů, kvůli kterým jsou voleny provozovateli satelitů
různé sklony dráhy. Například heliosynchronní dráha. Je to geocentrická
dráha kombinující sklon a výšku oběhu tak, že satelit přelétá nad určeným
povrchem Země vždy ve stejný sluneční čas, toto je velmi vhodné pro
mapující a špionážní satelity. Satelity na této dráze pracují často ve
výškách cca 600–800km a mají 98° sklon vůči rovníku.
RAAN - vzestupný úhel
("RAAN" nebo "RA uzlu" nebo "O0", a občas taky "Zeměpisná délka
vzestupného uzlu")
Dvě čísla orientují orbitální rovinu v prostoru. První číslo byla
Inklinace. RAAN je druhé číslo.
Poté, co jsme určili sklon, stále ještě
existuje nekonečné množství oběžných rovin. Linie vzestupných bodů
může vyčnívat kdekoli podél rovníku. Pokud určíme, kde podél rovníku
vyčnívá linie vzestupných bodů, budeme mít plně specifikovanou rovinu
oběžné dráhy. Řada bodů samozřejmě vyčnívá ze dvou míst. Stačí
specifikovat jeden z nich. Ten se nazývá vzestupný uzel (kde satelit
překračuje rovník z jihu na sever). Druhý se nazývá sestupný uzel (kde
satelit protíná rovník ze severu na jih). Podle konvence určíme umístění
vzestupného uzlu.
Země se však otáčí. To znamená, že nemůžeme použít společný souřadnicový
systém zeměpisné šířky a délky k určení, kam směřuje čára uzlů. Místo toho
používáme astronomický souřadnicový systém, známý jako souřadnicový systém
pravého vzestupu / deklinace, který se neotáčí se Zemí. Pravý vzestup je
slovo, které mi přeložil strejda Google. Jde o úhel měřený v rovníkové
rovině od referenčního bodu na obloze, kde je pravá rektascenze definována
jako nulová. Astronomové nazývají tento bod jarní rovnodennost. V obrázku
jsem napsal, že za referenční směr se považuje první bod (hvězda)
souhvězdí Berana (latinsky se řekne ovce Aries). Taky tohle ve škole uváděli jako úhel, tedy místo, ve
kterém vyjde sluníčko nad obzor na první jarní den.
Můžeme však použít lepší definici. Zvažte oběžnou dráhu Slunce kolem Země. Samozřejmě, že ve škole se učí, že Země obíhá kolem Slunce, ale matematika umí pracovat s relativním pohybem. Také se mu říká zdánlivý pohyb Slunce. V tuto chvíli vyhovuje našim potřebám, když si představíme Slunce obíhající kolem Země. Znovu opakuji, jde o zdánlivý pohyb Slunce po obloze. Oběžná dráha Slunce má sklon (inklinaci) asi 23,5 stupňů. (Mimochodem, astronomové nenazývají tento úhel 23,5 stupně "inklinací, sklonem". Používají nekonečně obskurní název: "The Obliquity of The Ecliptic" a i v naší zemi je znám termín ekliptika. Oběžná dráha Slunce byla lidmi rozdělena do čtyř stejně velkých částí nazývaných roční období. Ten, který se nazývá jaro, začíná, když slunce vyjde nad rovník. Jinými slovy, první jarní den je dnem, kdy Slunce prochází rovníkovou rovinou jdoucí z jihu na sever. Máme pro takový bod jméno. Je to vzestupný bod (uzel) oběžné dráhy Slunce. Takže konečně, jarní rovnodennost není nic jiného než vzestupný bod oběžné dráhy Slunce. Oběžná dráha Slunce má RAAN = 0 jednoduše proto, že jsme definovali vzestupný bod Slunce jako místo, od kterého jsou měřeny všechny vzestupné body. RAAN oběžné dráhy našeho satelitu je pouze úhel (měřený ve středu Země) mezi místem, kde oběžná dráha Slunce vyskočí nad rovník, a místem, kde oběžná dráha našeho satelitu vyskočí nad rovník.
Argument perigea (jde o označení
úhlu)
(také znám jako "ARGP" nebo "W0")
Prý jde jen o další módní slovo pro úhel pohledu. Protože už jsme
orientovali orbitální rovinu v prostoru, musíme orientovat elipsu oběžné
dráhy v orbitální rovině. Uděláme to zadáním jediného úhlu, kterému říkáme
argument perigea.
Pár slov o eliptických drahách... Bod, kde je satelit nejblíže k Zemi, se
nazývá perigeum. Bod, kde je satelit nejdále od Země, se nazývá apogeum.
Nakreslíme-li čáru od perigea k apogeu, nazývá se tato přímka apsid.
Apsidy je samozřejmě množné číslo od apsid. Na prvním obrázku je
nakreslena jen do středu Země. Prý se to podle autora a astronomů
zase komplikuje. V praxi se linie apsidů nazývá jako hlavní osa
elipsy. Je to jen čára nakreslená přes elipsu "dlouhou cestu".
Linie apsidů prochází středem země. Již jsme identifikovali další čáru
procházející středem Země: linii uzlů. Úhel mezi těmito dvěma přímkami se
nazývá argument perigea. Tam, kde se protínají jakékoli dvě přímky, tvoří
dva doplňkové úhly, takže abychom byli konkrétní, říkáme, že argument
perigea je úhel (měřený ve středu Země) od vzestupného uzlu k perigeu.
Příklad: Když ARGP = 0, perigeum se vyskytuje na stejném místě jako
vzestupný uzel. To znamená, že satelit by byl nejblíže k Zemi právě ve
chvíli, kdy stoupá nad rovník. Když ARGP = 180 stupňů, apogeum by se
vyskytovalo na stejném místě jako vzestupný uzel. To znamená, že satelit
by byl nejdále od Země právě ve chvíli, kdy stoupá nad rovník.
Podle konvence je ARGP úhel mezi 0 a 360 stupni.
|
Výstřednost Střední pohyb
|
|
|
Fáze, střední anomálie |
|
|
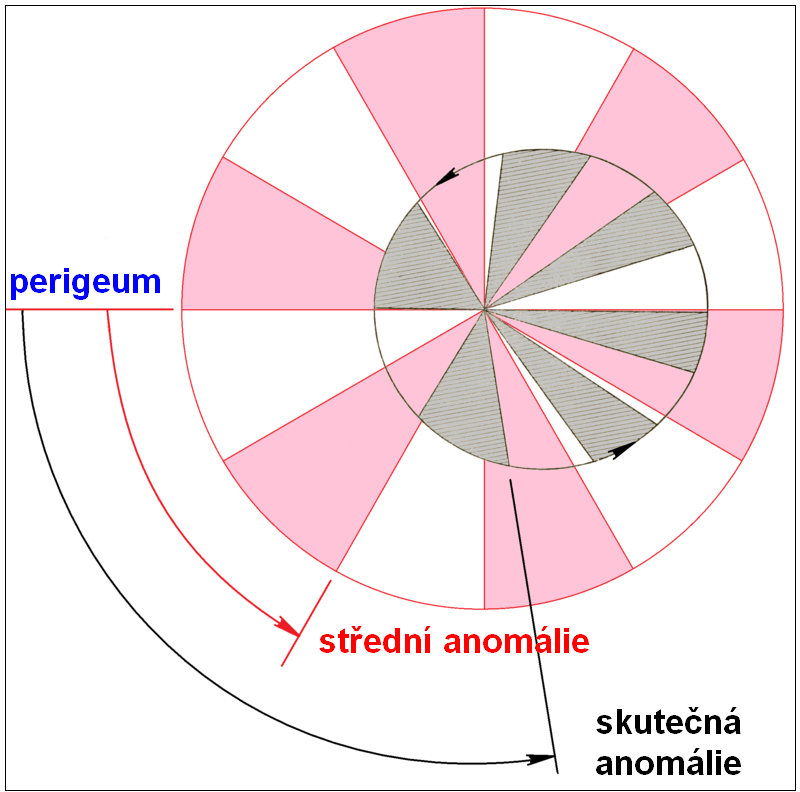
Na obrázku vpravo je znázorněn význam "střední anomálie", který přesně platí pro kruhovou dráhu a "skutečné anomálie", který platí pro konkrétní satelit s eliptickou dráhou. |
|
Drag - brždění
(také označován jako "N1")
Odpor způsobený zemskou atmosférou způsobuje, že satelity spirálovitě
klesají. Jak spirálovitě klesají, zvyšují svou rychlost - zrychlují.
Orbitální prvek Drag nám jednoduše říká rychlost, jakou se střední pohyb
mění v důsledku odporu nebo jiných souvisejících efektů. Přesně tak, Drag
je poloviční první derivace Mean Motion.
Jeho jednotky jsou otáčky za den za den. Obvykle se jedná o velmi malé
číslo. Běžné hodnoty pro satelity na nízké oběžné dráze Země jsou v řádu
10-4. Běžné hodnoty pro družice na vysoké oběžné dráze jsou
řádově 10-7 nebo menší.
Příležitostně publikované orbitální elementy pro satelit na vysoké oběžné
dráze ukazují negativní Drag! Zpočátku se to může zdát absurdní. Odpor
způsobený třením se zemskou atmosférou může způsobit spirálu satelitu
pouze směrem dolů, nikdy nahoru.
Existuje několik možných důvodů negativního odporu. Za prvé, měření, které
vytvořilo orbitální elementy, mohlo být chybné. Je běžné odhadovat
orbitální elementy z malého počtu pozorování provedených v krátkém časovém
období. S takovými měřeními je velmi obtížné odhadnout Drag. Velmi
obyčejné malé chyby v měření mohou způsobit malý negativní odpor.
Druhá potenciální příčina negativního odporu publikovaných prvků je trochu
složitější. Satelit je vystaven mnoha silám kromě dvou, o kterých jsme
dosud diskutovali (zemská gravitace a atmosférický odpor). Některé z
těchto sil (například gravitace Slunce a Měsíce) mohou působit společně a
způsobit, že satelit bude vytažen nahoru o velmi malé množství. K tomu
může dojít, pokud jsou Slunce a Měsíc určitým způsobem zarovnány s oběžnou
dráhou satelitu. Pokud je oběžná dráha měřena, když se to děje, malý
záporný výraz Drag může ve skutečnosti poskytnout nejlepší možné
"přizpůsobení" skutečnému pohybu satelitu za krátké časové období.
Obvykle chcete sadu orbitálních elementů, abyste stanovili polohu satelitu
přiměřeně dobře po co nejdelší dobu, často několik měsíců. Negativní odpor
nikdy přesně neodráží to, co se děje po dlouhou dobu. Některé programy
akceptují záporné hodnoty pro Drag, ale nemusí to být dobře. Doporučuje se
nahradit nulou jakoukoli publikovanou zápornou hodnotou drag.
Ostatní parametry
Epocha Rev
(též "Revolution Number at Epoch")
To říká sledovacímu programu, kolikrát satelit obíhal od doby, kdy byl
vypuštěn, do času určeného hodnotou "Epoch". Epoch Rev se používá k
výpočtu čísla oběhu zobrazeného sledovacím programem. Nebuďte překvapeni,
pokud zjistíte, že sady orbitálních prvků, které pocházejí z NASA, nemají
správné hodnoty pro Epoch Rev. Lidé, kteří počítají oběžné dráhy satelitů,
nemají tendenci věnovat tomuto číslu velkou pozornost!
Attitude (ve významu postoj k pozorovateli, k Zemi, jde o směrování
antén)
(taky "Souřadnice Bahn")
Poloha kosmické lodi je měřítkem toho, jak je satelit orientován ve
vesmíru. Doufejme, že je orientován tak, aby jeho antény směřovaly k vám!
V satelitech se používá několik orientačních schémat. Souřadnice Bahn
platí pouze pro kosmické lodě, které jsou spin-stablized. Spinově
stabilizované satelity udržují konstantní inerciální orientaci, tj. jejich
antény směřují v prostoru pevným směrem (příklady z historie: Oscar-10,
Oscar-13).
Souřadnice Bahn se skládají ze dvou úhlů, často nazývaných Bahn Latitude a
Bahn Longitude. Ty jsou čas od času publikovány pro amatérské rádiové
družice na eliptické dráze v různých amatérských družicových zdrojích.
V ideálním případě zůstávají tato čísla konstantní, s výjimkou případů,
kdy řídící jednotky kosmické lodi mění orientaci kosmické lodi. V praxi se
pohybují pomalu.
Pro vysoce eliptické dráhy (Oscar-10, Oscar-13 atd.) byla tato čísla
obvykle v blízkosti: 0,180. To znamená, že antény směřovaly přímo k Zemi,
když byl satelit v apogeu.
Tato dvě čísla popisují směr ve sférickém souřadnicovém systému, stejně
jako zeměpisná šířka a délka popisují směr od středu Země. V tomto případě
je však primární osa podél vektoru od satelitu ke středu Země, když je
satelit v perigeu.
Příklad uváděného formátu TLE dat
Příklad je uveden např. zde: Two-line element set - Wikipedia
ISS (ZARYA)
1 25544U 98067A 08264.51782528 -.00002182 00000-0 -11606-4 0 2927
2 25544 51.6416 247.4627 0006703 130.5360 325.0288 15.72125391563537
význam je uveden na původní stránce.
Já si stahuji data na
CelesTrak
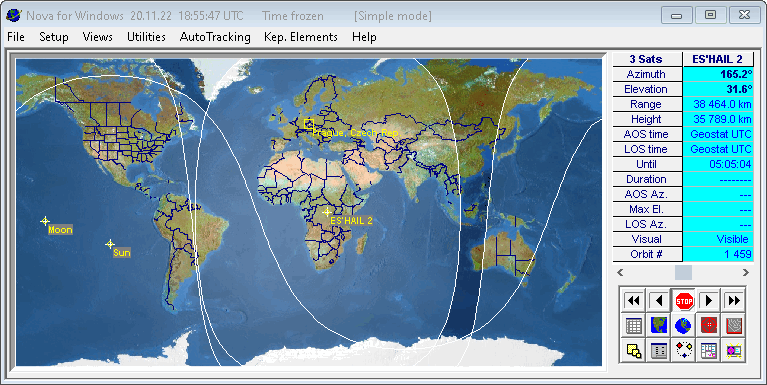
kde je možnost prohlížet data celé řady satelitů. Program Nova for
Windows, který používám mám nastaven rovněž na aktualizaci dat z tohoto
serveru.
Některé odkazy k popisované problematice na wikipedii
https://en.wikipedia.org/wiki/Longitude_of_the_ascending_node
https://en.wikipedia.org/wiki/Orbital_eccentricity
https://en.wikipedia.org/wiki/Argument_of_periapsis
https://commons.wikimedia.org/wiki/File:Mean_anomaly_diagram.png
https://en.wikipedia.org/wiki/Mean_motion
https://en.wikipedia.org/wiki/Kepler%27s_equation
Čím polohu satelitu počítat?
Existuje několik programů a několik on-line služeb. Zde jsou 3 odkazy na
ty rozšířené:
https://www.nlsa.com/
http://www.dk1tb.de/indexeng.htm
https://www.n2yo.com/
| Protože je mnoho podobných služeb a programů, určitě si každý najde svůj oblíbený. Já používám
Nova for Windows (stažený
z prvního odkazu). Rovněž jsem ho dal ke
stažení z
této stránky (server nagano.cz) - jedná se o archiv
zip, který obsahuje instalační soubor, textový soubor s heslem a
program patch.exe pro novější systémy Windows. Archiv si rozbalíme,
spustíme instalační program. Během instalace zadáme heslo. Program
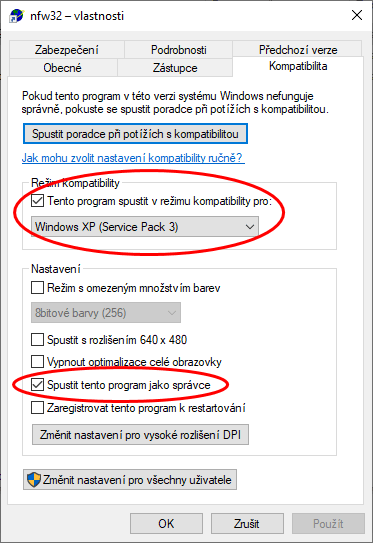
však nespouštíme a nainstalujeme ještě program patch. Po instalaci
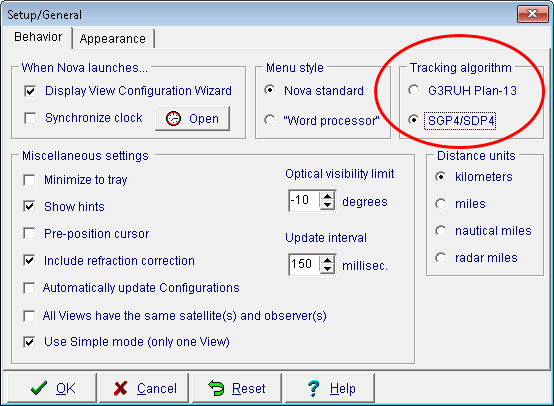
nastavíme u programu nejdřív vlastnosti - obrázek vpravo. Program
doporučuji spouštět v režimu kompatibility Windows XP a spouštět jako
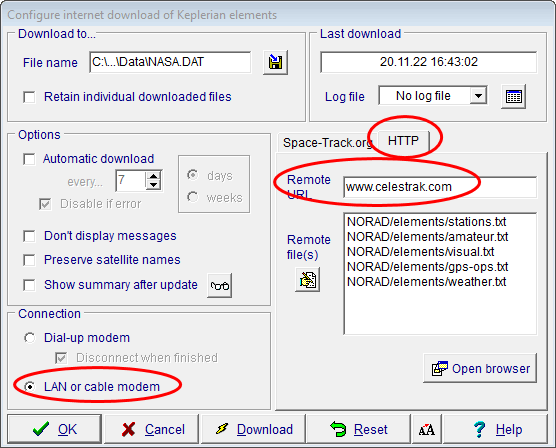
správce). Poté, co se s programem seznámíme, provedeme update
Keplerian dat:
|
|
|
Algoritmus výpočtu pozice satelitu z keplerovských dat (řešení Keplerovských rovnic) |
|
|
Ostatní nastavení se týkají toho, aby program počítal a zobrazoval informace, které potřebujeme. Obrázek pro ilustraci. Fakt to počítá parametry orbity a celou řadu dalších věcí z keplerovských dat.
|
|
Související téma
S mechanikou pohybu satelitu souvisí gravitační zákon. Jde o téma, které bylo mnohokrát popsáno a možná i já mu jednou budu věnovat trochu času. Na Internetu jsem však našel na stánce: Impuls síly Impuls síly: pokud je síla konstatní - ppt stáhnout (slideplayer.cz) celkem slušně udělanou prezentaci k danému tématu. V prezentaci nechybí matematický základ, který popisuje princip impulsu síly, změny hybnosti tělesa, gravitační zákon a několik dalších zajímavých informací, které přímo nesouvisejí se satelity (slapové síly, Rocheův limit). Ke stažení v pdf dávám zde.
Závěr
Cílem článku bylo shrnout na jedno místo pár základních informací, které
se týkají významu tzv. keplerovských dat (Keplerian elements) pro
stanovení polohy satelitu.