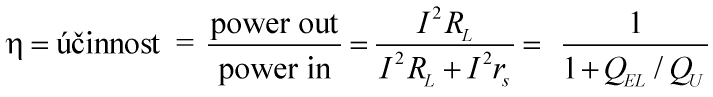Porovnání ztrát u různého napájení deltaloopu

další info >>>>

Kontakt

Provnání ztrát u různého způsobu napájení deltaloopu

.........................................................................................................................................................................................................................................................................................................

Všeobecně

Motivací k tomuto článku byly celkem tři věci. Jednak to byly reakce na mé publikované články, které se týkaly napájení vícepásmové antény delta loop koaxiálním kabelem. Tady si myslím, že mám dluh ve vysvětlení, za jakých podmínek lze deltaloop koaxiálním napáječem napájet. Druhou motivací je, abych znovu ukázal, jak na výpočet ztrát v napáječi jít jednoduše a prakticky, abych ukázal, jak je na tom ten zmíněný způsob napájení koaxem. A třetí motivací je, abych vám k tomuto přemýšlení zadal jednoduchou prázdninovou úlohu. Tentokrát praktickou.

Ztráty v napáječi a v transformaci impedancí

U antény deltaloop nemohu řešit jednu věc bez druhé, protože tato anténa zpravidla nemá impedamci v bodě napájení Z=50 Ohmů. Pro základní vysvětlení ztrát v napájení použiji příklady. Na prvních příkladech, které se budou lišit zejména způsobem napájení, použiji předpoklad, že impedance na svorkách antény je R=100 Ohmů a jX=0. Na dalších příkladech budu pracovat se skutečnou impedancí mého deltaloopu - viz tabulka. Vzorec pro výpočet ztrát převezmu z mého dříve publikovaného článku:

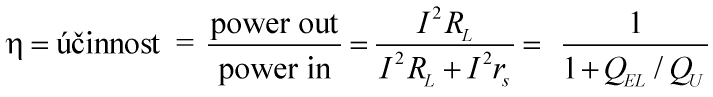
Zopakuji, že pro nejvyšší účinnost přenosu energie se musí jmenovatel zlomku blížit k jedničce. To znamená, že Q_EL/Q_U se budeme snažit udělat nulové. Jak toho docílíme? Pokud chceme být úspěšní, potom využijeme obou cest. Budeme se snažit dělat co nejmenší jakost Q_EL zatíženého napájecího obvodu a naopak, používat co největší jakost - Q-Factor nezatížené komponenty (indukčnost, transformační vedení).

Jakost transformačního obvodu řešíme ve Smithově diagramu

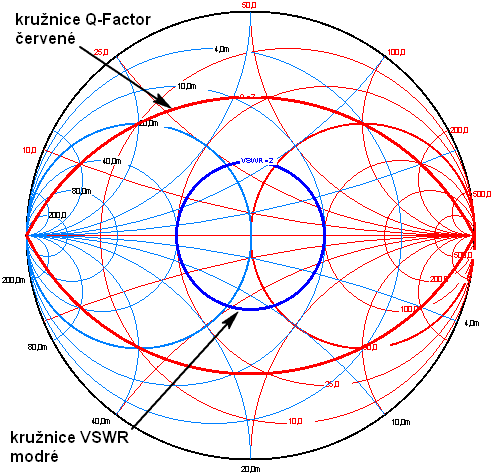
1. Pro tento článek jsem použil netypické barvy kružnic (aby byly vidět i slepými, hi). Kružnice jakosti Q zatíženého transformačního obvodu jsou označené červeně, viz obrázek vlevo, zakreslena kružnice Q = 7. Na tomtéž obrázku je zakreslena modře kružnice VSWR = 2. Na dalších obrázcích budou ještě vidět kružnice komponent, tj. vedení (koaxiální kabel) a LC přizpůsobovacích obvodů tuneru.
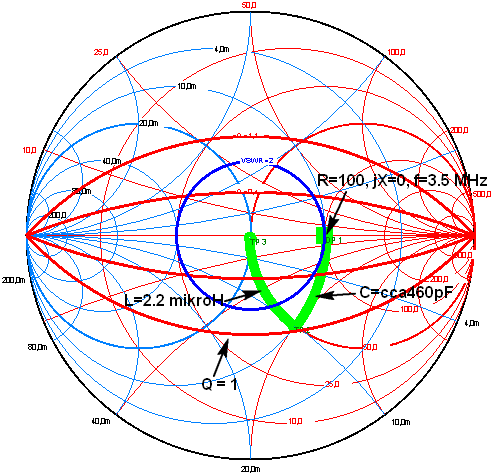
2. Na kmitočtu 3,5 MHz má náš delta loop impedanci Z = 100+j0 a snadno ho na tomto kmitočtu přizpůsobíme kapacitou 460 pF a indukčností 2,2 mikrohenry. Vidíme, že tento jednoduchý L článek má Q zatíženého obvodu Q_EL = 1, což je vidět z obrázku vpravo, spodní červená čára Q_EL=1 se nám dotýká v bodě TP2 .... Známe-li jakost nezatíženého induktoru L, můžeme vypočítat ztráty.
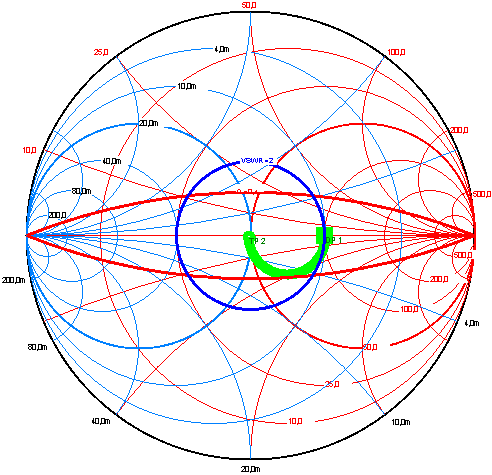
3. Stejný deltaloop můžeme přizpůsobit koaxiálem o charakteristické impedanci Z0 = 70 Ohmů. Délka takového koaxiálu musí být 0.25 x lambda a z obrázku vidíte, že Q_EL=0.4. Tuto čáru jsem mimochodem zakreslil i do předchozího diagramu. Ryze z pedagogických důvodů, pro perfekcionisty, aby věděli, že použití L článku pro přizpůsobení byl jen jejich kompromis. Proboha, netvrdím zde, že tento přizpůsobovací obvod má nižší ztráty než ten předchozí. Velikost ztrát u obou případů je dána ještě druhým číslem ve zlomku - sice jakostí nezatíženého obvodu (indukčnosti v prvním případě, čtvrtvlnového obvodu z koaxiálu v tomto případě).
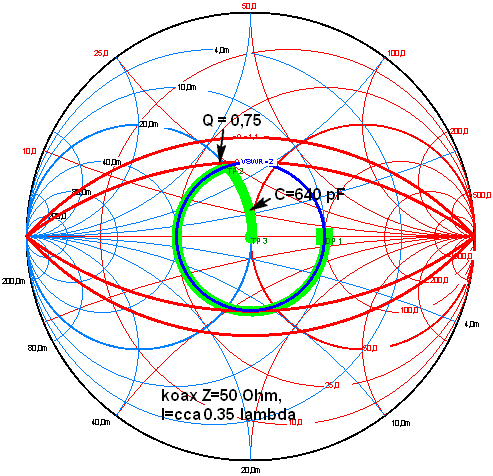
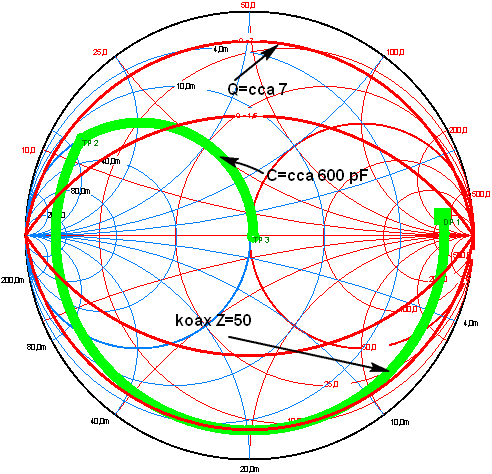
4. Co se stane, když použijeme koaxiál Z=50 Ohmů? Jen s koaxiálem nepřizpůsobíme. Při jeho vhodné délce, viz obrázek vedle (asi 0.35 x lambda) však redukujeme L článek na jednu jedinou kapacitu C = 640 pF. Při tomto způsobu transformace vidíte, že Q_EL= 0.75, což je stále méně, než v případu 2. Poznámka: koaxiální kabel Z=50 Ohmů je reprezentován zelenou kružnicí kolem středu diagramu.
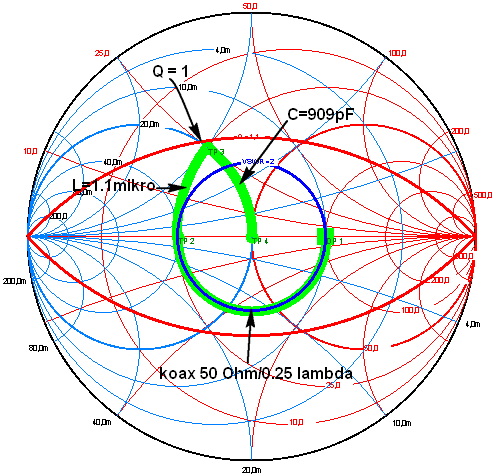
5. Příklad jen pro ilustraci. Pokud by byl delta loop napájen jen koaxiálem dlouhým 0.25 x lambda, musel by být přizpůsoben L článkem s hodnotami L=1,1 mikrohenry a C asi 900 pF. V takovém případě je Q_EL = přibližně 1.
Ztráty transformačního obvodu jsou však definovány vzorcem, který jsem uvedl v úvodu. Opakuji, že jsou dány poměrem Q_EL/Q_U, který musí být co nejmenší. Na předchozích příkladech jsem uvedl několik způsobů řešení transformačního a napájecího obvodu a stanovení hodnoty Q_EL ve Smithově diagramu. Ale v úvodu jsem napsal, že mojí třetí motivací je zadání jednoduché prázdninové úlohy. Její zadání zní: "Jak jednoduše pomocí VNA analyzátoru stanovit jakost Q (Q-Factor) indukčnosti tuneru a kusu koaxiálního kabelu?" Po prázdninách sem dám samozřejmě odkaz, jak to dělám já. Na Internetu však najdete několik dobrých návodů o tom, jak se to dělá. Závěr k první části Až budete znát hodnoty jakostí nezatížených součástí (indukčnost L článku, vedení z koaxiálu) a hodnoty impedancí vašeho delta loopu, bude znát rovněž ztráty v napájení. A budete moci posoudit, zda moje tvrzení o napájení deltaloopu koaxiálem bylo odvážné, či nikoliv. Vícepásmový deltaloop V této části se vracím k prvotní motivaci, tj. k odvážnému tvrzení o přizpůsobení deltaloopu na všech pásmech.
6. Jeden z posledních deltaloopů, které jsem v QTH Nové Hodějovice používal, měl impedance uvedené v tabulce vpravo vedle tohoto textu. Jde o změřené hodnoty. Já jsem ho napájel krátkým koaxiálním kabelem, na jehož konci byl balun s transformačním poměrem 1:4. Delta loop byl situován tak, že jsem místo napájení měl asi 2m od tuneru a mohl jsem srovnat v praxi různé způsoby napájení a přizpůsobení. Nejhorší VSWR měl můj deltaloop na pásmu 17m a hodnoty jsem v tabulce zdůraznil. Všimněte si ještě pro zajímavost hodnot jX v pásmech 80m, 40m, 20m, 15m a 10m. Pouze na 40m byla rezonance nepatrně mimo pásmo.
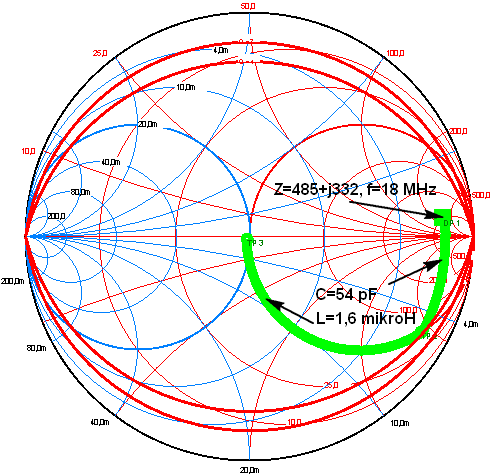
7. Na pásmu 17m šel deltaloop přizpůsobit jednoduchým L článkem s rozumnými hodnotami C=54 pF a L=1.6 mikrohenry. Z hlediska ztrát je důležitý Q_EL = cca 4. Tedy mnohem více, než například v pásmu 80 metrů, kde Q_EL = 1. Při stejné jakosti induktoru Q = 100 by nám vyšla účinnost asi 96%, kdežto v příkladě 2 by to bylo asi 99%.
8. Rovněž na pásmu 17m si vyřešíme Q_EL , a to pro případ, že ke smyčce připojíme koaxiální kabel napřímo, ale uděláme ho současně rezonující, tak, abychom v L článku již potřebovali jen kondenzátor. V tomto případě nám vyleze Q_EL na hodnotu Q_EL = 7. Pro informaci zde uvedu ještě účinnosti takového napájení pro tři hodnoty Q_Unezatíženého koaxiálu: Q_U = 10, účinnost = 58% Q_U = 20, účinnost = 74% Q_U = 50, účinnost = 87% Q_U = 100, účinnost = 93% Až budete mít změřené hodnoty jakostí Q u kabelů, které používáte, budete již vědět, s jakou účinností jste tímto způsobem deltaloop přizpůsobili, ale již nyní tušíte, že koaxiál s mizerným Qu nám tratí 58% energie (asi -2.4 dB).
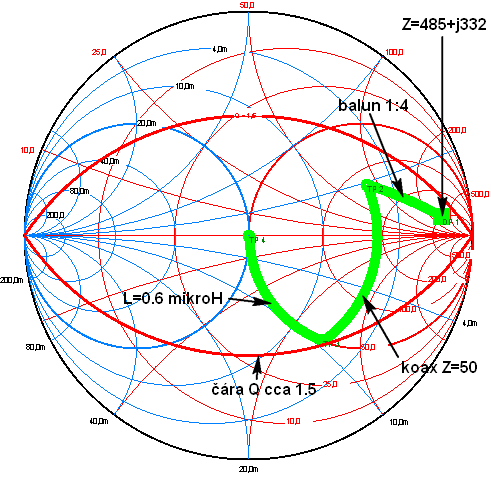
9. Opět máme pásmo 17m a použijeme balun 1:4, koaxiál 50 Ohmů a pro změnu indukčnost v tuneru. Vše zakresleno do obrázku vpravo vedle textu. Čára Q_EL = jenom asi 1.5 Zkuste si udělat úvahu o maximálních ztrátách.
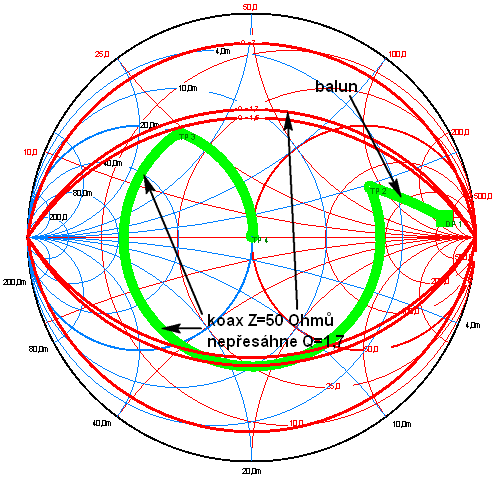
10. Opět stejné pásmo 17 metrů a stejné hodnoty impedance. Ladíme však delším koaxiálm (asi 5 metrů) i impedanci 50 Ohmů a pouze kapacitou v tuneru. Opět Q_EL nepřesáhne hodnotu 1.7
Shrnutí k druhé části úloh V první části jsem řešil různé způsoby přizpůsobení delta loopu v rezonanci.
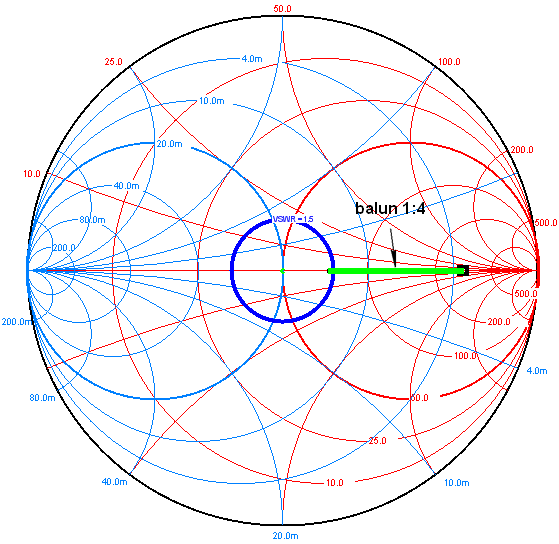
11. Pro úplnost uvedu ještě příklad reálné antény (viz tabulka), která má na svorkách jen balun. V diagramu je zakreslena kružnice VSWR = 1.4 Uvedený příklad je pro skutečnou anténu a pásmo 20m. Pouhé použití balunu nám zabezpečí hodnotu VSWR = 1.4
Ve druhé části jsem ukázal na pásmu 17m, které je skutečně velice vzdáleno od rezonance, co by se mělo alespoň orientačně, a to i v amatérských podmínkách vyřešit, aby nám ztráty nesežraly veškerou energii. Znovu opakuji, anténa byla konstruována tak, aby rezonovala na 80/40/20/15 a 10 metrech - viz tabulka a úvaha je o tom, s jakými ztrátami ji lze vyladit na 17 metrech. Obdobně by se to řešilo na 30m i na 12 metrech. A ukázal jsem, že s koaxiálem, který bude mít nízkou jakost Q si klidně ztratím tím, že přijmu tento kompromis -2.3 dB. Je tedy na místě uvést, jak vlastně ta anténa vyzařuje na pásmu 17m:


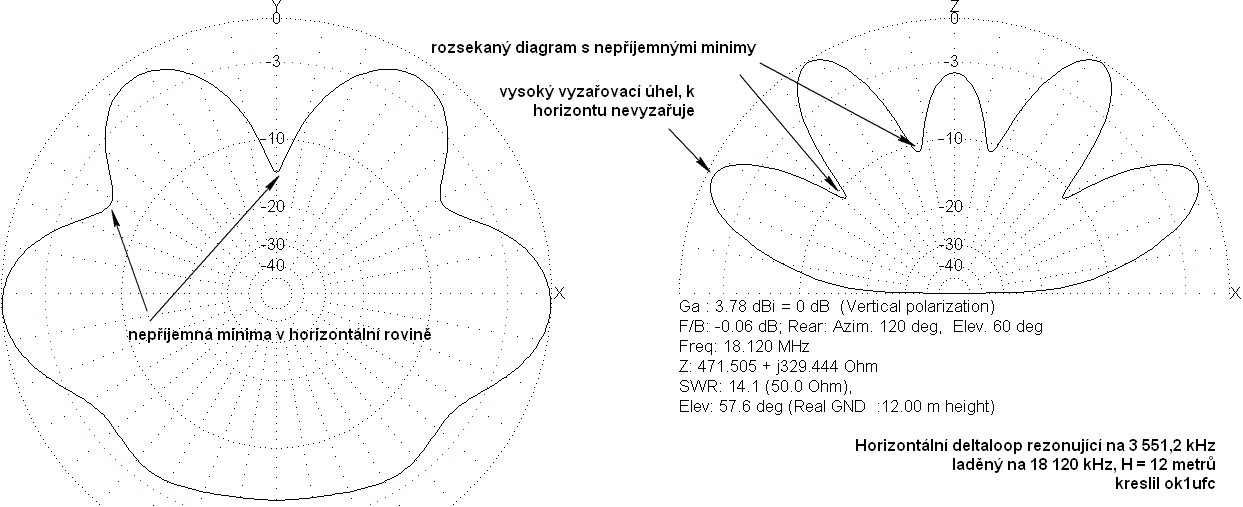A vidíte, stejně, jako já, že sice minimalizací důsledků ztrát v napáječi a tuneru vyřešíme ztráty kolem 3 dB, ale navržená anténa nám stejně vysíla směrem k horizontu (na elevaci 5°) s potlačením -15 dB, má v horizontální rovině nepříjemná minima až -15 dB a ve vertikální rovině je rovněž mnoho minim kolem -10 dB, možná větších.
Moje poznámky
a) myslím, že kvantifikace ztrát v napáječi antény deltaloop si zasloužila více slov a mé pozornosti, rád jsem zde uvedl několik příkladů s konkrétními čísly a částečně napravil můj dluh b) je třeba si uvědomit, že konkrétní anténa byla poměrně přesně nastavená do rezonance na základních pásmech c) chtěl jsem zopakovat a na příkladech ukázat, že každý přizpůsobovací čtyřpól je kompromis a má ztráty, a to včetně oblíbeného L článku; na reálných příkladech jsem vám ukázal, že i L článek má konkrétní hodnotu Q_EL , která se na ztrátách podílí d) a chci znovu zopakovat, že koaxiální kabely jsou opravdu vhodné pro napájení antén postupnou vlnou, nikoliv pro napájení stojatou vlnou. Pokud je pro takový případ použijete, děláte kompromis a je důležité tyto ztráty řešit, kvantifikovat a porovnat s jinými druhy ztrát. V uvedených příkladech jsem ukázal, jak jsem to řešil na deltaloopu. Přesto bych byl nerad, aby některé jiné vlastnosti antény delta loop byly přisuzovány jen ztrátám v napáječi. e) Chtěl jsem, aby toto téma bylo věnováno delta loopům, nikoliv koaxiálům. Přesto si zde neodpustím malou poznámku, která se týká stojatého vlnění. Jak jsem již v několika článcích napsal, na krátkých vlnách se často používají rezonanční antény. Ty vždy pracují se stojatou vlnou. Některé konstrukce antén využívají rovněž napáječe se stojatou vlnou (např. G5RV, Single Zeppelin, Double Zeppelin, lze tak zkonstruovat i delta loop). Samostatným tématem (nikoliv tohoto článku) je řešení rozložení vln (přímé a odražené) na vedení. Jde nám o rozložení napětí a proudů. Víme, že rozložení napětí a proudů je dáno vektorovým součtem obou výše uvedených vln. Při přenosu stejného výkonu nám vznikají u vedení se stojatými vlnami většín ztráty energie proti vedení jen s postupnou vlnou. Na internetu najdete různé kalkulátory, které vám vypočítají ztráty v koaxiálním vedení, pokud jsou na vedení stojaté vlny. Jak jsem již napsal v bodě d) koaxiál se stojatou vlnou je také kompromis, ale je dobré umět s takovým kompromisem dělat, nejen prakticky, ale i s minimem teorie. Jen tak si vytvoříme správný názor na to, jaké rozdíly v různých kompromisních řešeních jsou. V některém z podzimních článků popíšu mé jednoduché metody měření jakosti Q pro některé konfigurace pahýlů a přizpůsobovacích obvodů z koaxiálů. Tedy to, co jsem zde zadal jako prázdninové cvičení. Je to poslední veličina, kterou zatím pro jednoduchý výpočet ztrát z mých článků neznáte. Přeji vám hezký zbytek letošních prázdnin. V Českých Budějovicích, 4.8.2014